一、卷积神经网络的概述

卷积神经网络（ConvolutionalNeural Network，CNN）最初是为解决图像识别等问题设计的，CNN现在的应用已经不限于图像和视频，也可用于时间序列信号，比如音频信号和文本数据等。CNN作为一个深度学习架构被提出的最初诉求是降低对图像数据预处理的要求，避免复杂的特征工程。在卷积神经网络中，第一个卷积层会直接接受图像像素级的输入，每一层卷积（滤波器）都会提取数据中最有效的特征，这种方法可以提取到图像中最基础的特征，而后再进行组合和抽象形成更高阶的特征，因此CNN在理论上具有对图像缩放、平移和旋转的不变性。

卷积神经网络CNN的要点就是局部连接（LocalConnection）、权值共享（Weights Sharing）和池化层（Pooling）中的降采样（Down-Sampling）。其中，局部连接和权值共享降低了参数量，使训练复杂度大大下降并减轻了过拟合。同时权值共享还赋予了卷积网络对平移的容忍性，池化层降采样则进一步降低了输出参数量并赋予模型对轻度形变的容忍性，提高了模型的泛化能力。可以把卷积层卷积操作理解为用少量参数在图像的多个位置上提取相似特征的过程。

卷积层的空间排列：上文讲解了卷积层中每个神经元与输入数据体之间的连接方式，但是尚未讨论输出数据体中神经元的数量，以及它们的排列方式。3个超参数控制着输出数据体的尺寸：深度（depth），步长（stride）和零填充（zero-padding）。首先，输出数据体的深度是一个超参数：它和使用的滤波器的数量一致，而每个滤波器在输入数据中寻找一些不同的东西。其次，在滑动滤波器的时候，必须指定步长。有时候将输入数据体用0在边缘处进行填充是很方便的。这个零填充（zero-padding）的尺寸是一个超参数。零填充有一个良好性质，即可以控制输出数据体的空间尺寸（最常用的是用来保持输入数据体在空间上的尺寸，这样输入和输出的宽高都相等）。输出数据体在空间上的尺寸可以通过输入数据体尺寸（W），卷积层中神经元的感受野尺寸（F），步长（S）和零填充的数量（P）的函数来计算。（这里假设输入数组的空间形状是正方形，即高度和宽度相等）输出数据体的空间尺寸为(W-F +2P)/S+1，在计算上，输入数据体的长和宽按照该公式计算，深度依赖于滤波器的数量。步长的限制：注意这些空间排列的超参数之间是相互限制的。举例说来，当输入尺寸W=10，不使用零填充则P=0，滤波器尺寸F=3，这样步长S=2就行不通，结果4.5不是整数，这就是说神经元不能整齐对称地滑过输入数据体。

汇聚层使用MAX操作，对输入数据体的每一个深度切片独立进行操作，改变它的空间尺寸。最常见的形式是汇聚层使用尺寸2x2的滤波器，以步长为2来对每个深度切片进行降采样，将其中75%的激活信息都丢掉。每个MAX操作是从4个数字中取最大值（也就是在深度切片中某个2x2的区域）。深度保持不变。

二、卷积神经网络的结构

卷积神经网络通常是由三种层构成：卷积层，汇聚层（除非特别说明，一般就是最大值汇聚）和全连接层（fully-connected简称FC）。ReLU激活函数也应该算是是一层，它逐元素地进行激活函数操作。

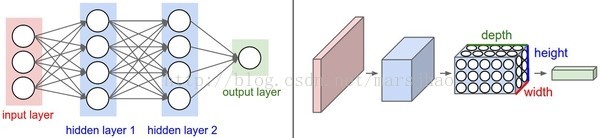
卷积神经网络最常见的形式就是将一些卷积层和ReLU层放在一起，其后紧跟汇聚层，然后重复如此直到图像在空间上被缩小到一个足够小的尺寸，在某个地方过渡成成全连接层也较为常见。最后的全连接层得到输出，比如分类评分等。

最常见的卷积神经网络结构如下：

INPUT -> [[CONV -> RELU]*N ->POOL?]*M -> [FC -> RELU]*K -> FC

其中*指的是重复次数，POOL?指的是一个可选的汇聚层。其中N >=0,通常N<=3,M>=0,K>=0,通常K<3。

几个小滤波器卷积层的组合比一个大滤波器卷积层好。直观说来，最好选择带有小滤波器的卷积层组合，而不是用一个带有大的滤波器的卷积层。前者可以表达出输入数据中更多个强力特征，使用的参数也更少。唯一的不足是，在进行反向传播时，中间的卷积层可能会导致占用更多的内存。

输入层（包含图像的）应该能被2整除很多次。常用数字包括32（比如CIFAR-10），64，96（比如STL-10）或224（比如ImageNet卷积神经网络），384和512。

卷积层应该使用小尺寸滤波器（比如3x3或最多5x5），使用步长S=1。还有一点非常重要，就是对输入数据进行零填充，这样卷积层就不会改变输入数据在空间维度上的尺寸。一般对于任意F，当P=(F-1)/2的时候能保持输入尺寸。如果必须使用更大的滤波器尺寸（比如7x7之类），通常只用在第一个面对原始图像的卷积层上。

汇聚层负责对输入数据的空间维度进行降采样，提升了模型的畸变容忍能力。最常用的设置是用用2x2感受野的最大值汇聚，步长为2。注意这一操作将会把输入数据中75%的激活数据丢弃（因为对宽度和高度都进行了2的降采样）。另一个不那么常用的设置是使用3x3的感受野，步长为2。最大值汇聚的感受野尺寸很少有超过3的，因为汇聚操作过于激烈，易造成数据信息丢失，这通常会导致算法性能变差。

三、CNN最大的特点在于卷积的权值共享（参数共享），可以大幅度减少神经网络的参数数量，防止过拟合的同时又降低了神经网络模型的复杂度。如何理解？

假设输入图像尺寸是1000*1000并且假定是灰度图像，即只有一个颜色通道。那么一张图片就有100万个像素点，输入维度就是100万。如果采用全连接层（Fully Connected Layer，FCL）的话，隐含层与输入层相同大小（100万个隐含层节点），那么将产生100万*100万=1万亿个连接，仅此就有1万亿个参数需要去训练，这是不可想象的。考虑到人的视觉感受野的概念，每一个感受野只接受一小块区域的信号，每一个神经元不需要接收全部像素点的信息，只需要接收局部像素点作为输入，而将所有这些神经元接收的局部信息综合起来就可以得到全局的信息。于是将之前的全连接模式修改为局部连接，假设局部感受野大小是10*10，即每个隐含节点只与10*10个像素点相连，那么现在只需要10*10*100万=1亿个连接了，相比之前的1万亿已经缩小了10000倍。假设我们的局部连接方式是卷积操作，即默认每一个隐含节点的参数都完全一样，那么我们的参数将会是10*10=100个。不论图像尺寸有多大，都是这100个参数，即卷积核的尺寸，这就是卷积对减小参数量的贡献。这也就是所谓的权值共享。我们采取增加卷积核的数量来多提取一些特征，每一个卷积核滤波得到的图像就是一类特征的映射，即一个Feature Map。一般来说，我们使用100个卷积核在第一个卷积层就足够了，这样我们有100*100=10000个参数相比之前的1亿又缩小了10000倍。卷积的好处是，不管图片尺寸如何，需要训练的参数数量只跟卷积核大小和数量有关，并且需要注意的是，尽管参数的数量大大下降了，但是我们的隐含节点的数量并没有下降，隐含节点的数量只跟卷积的步长有关系。

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持【听图阁-专注于Python设计】。