Python处理菜单消息操作示例【基于win32ui模块】
本文实例讲述了Python处理菜单消息操作。分享给大家供大家参考,具体如下:
一、代码
# -*- coding:utf-8 -*-
#! python3
import win32ui
import win32api
from win32con import *
from pywin.mfc import window
class MyWnd(window.Wnd):
def __init__ (self):
window.Wnd.__init__(self,win32ui.CreateWnd())
self._obj_.CreateWindowEx(WS_EX_CLIENTEDGE,\
win32ui.RegisterWndClass(0,0,COLOR_WINDOW+1),\
'www.jb51.net - MFC GUI',WS_OVERLAPPEDWINDOW,\
(10,10,800,500),None,0,None)
submenu = win32ui.CreateMenu()
menu = win32ui.CreateMenu()
submenu.AppendMenu(MF_STRING,1051,'&Open')
submenu.AppendMenu(MF_STRING,1052,'&Close')
submenu.AppendMenu(MF_STRING,1053,'&Save')
menu.AppendMenu(MF_STRING|MF_POPUP,submenu.GetHandle(),'&File')
self._obj_.SetMenu(menu)
self.HookCommand(self.MenuClick,1051)
self.HookCommand(self.MenuClick,1052)
self.HookCommand(self.MenuClick,1053)
def OnClose(self):
self.EndModalLoop(0)
def MenuClick(self,lParam,wParam):
if lParam == 1051:
self.MessageBox('Open','Python',MB_OK)
elif lParam == 1053:
self.MessageBox('Sava','python',MB_OK)
else:
self.OnClose()
w = MyWnd()
w.ShowWindow()
w.UpdateWindow()
w.RunModalLoop(1)
二、运行效果:
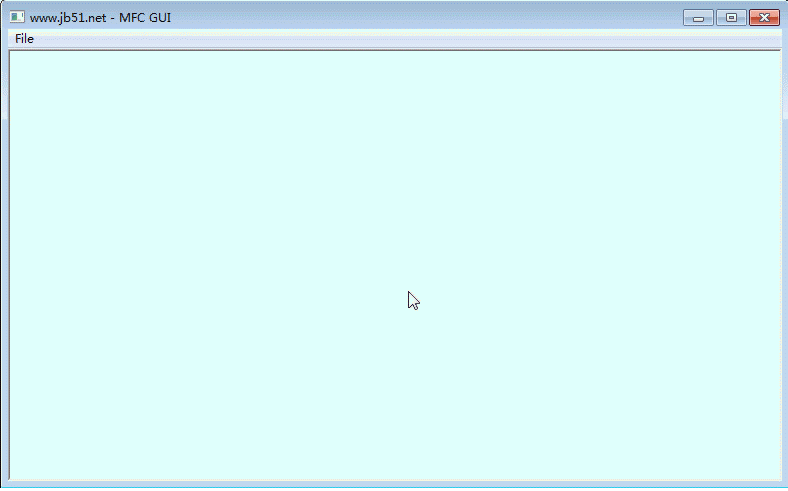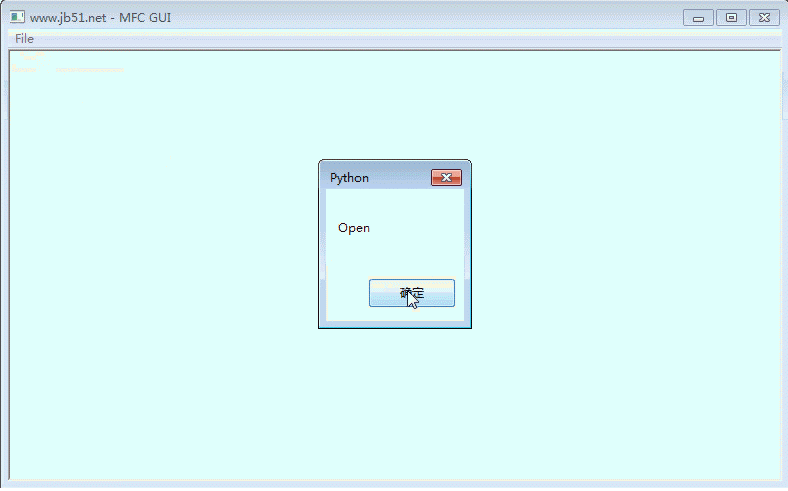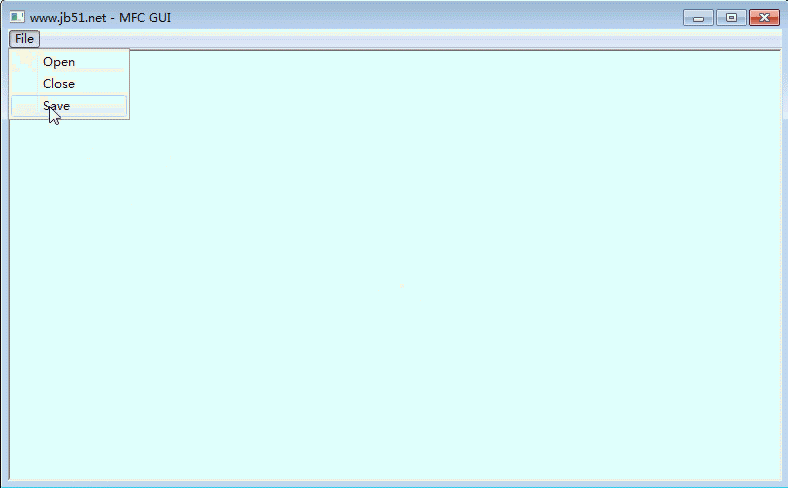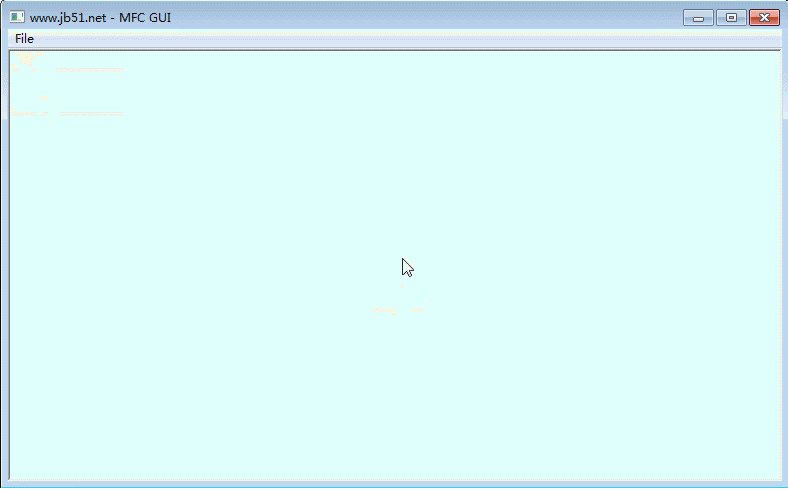
注:win32ui模块的安装可直接使用pip命令,如下:
pip install pypiwin32
更多关于Python相关内容感兴趣的读者可查看本站专题:《Python数据结构与算法教程》、《Python Socket编程技巧总结》、《Python函数使用技巧总结》、《Python字符串操作技巧汇总》、《Python入门与进阶经典教程》及《Python文件与目录操作技巧汇总》
希望本文所述对大家Python程序设计有所帮助。
