跟老齐学Python之集合的关系
冻结的集合
前面一节讲述了集合的基本概念,注意,那里所涉及到的集合都是可原处修改的集合。还有一种集合,不能在原处修改。这种集合的创建方法是:
>>> f_set = frozenset("qiwsir") #看这个名字就知道了frozen,冻结的set
>>> f_set
frozenset(['q', 'i', 's', 'r', 'w'])
>>> f_set.add("python") #报错
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
AttributeError: 'frozenset' object has no attribute 'add'
>>> a_set = set("github") #对比看一看,这是一个可以原处修改的set
>>> a_set
set(['b', 'g', 'i', 'h', 'u', 't'])
>>> a_set.add("python")
>>> a_set
set(['b', 'g', 'i', 'h', 'python', 'u', 't'])
集合运算
先复习一下中学数学(准确说是高中数学中的一点知识)中关于集合的一点知识,主要是唤起那痛苦而青涩美丽的回忆吧,至少对我是。
元素与集合的关系
元素是否属于某个集合。
>>> aset set(['h', 'o', 'n', 'p', 't', 'y']) >>> "a" in aset False >>> "h" in aset True
集合与集合的纠结
假设两个集合A、B
A是否等于B,即两个集合的元素完全一样
在交互模式下实验
>>> a set(['q', 'i', 's', 'r', 'w']) >>> b set(['a', 'q', 'i', 'l', 'o']) >>> a == b False >>> a != b True
A是否是B的子集,或者反过来,B是否是A的超集。即A的元素也都是B的元素,但是B的元素比A的元素数量多。
实验一下
>>> a set(['q', 'i', 's', 'r', 'w']) >>> c set(['q', 'i']) >>> c<a #c是a的子集 True >>> c.issubset(a) #或者用这种方法,判断c是否是a的子集 True >>> a.issuperset(c) #判断a是否是c的超集 True >>> b set(['a', 'q', 'i', 'l', 'o']) >>> a<b #a不是b的子集 False >>> a.issubset(b) #或者这样做 False
A、B的并集,即A、B所有元素,如下图所示

>>> a set(['q', 'i', 's', 'r', 'w']) >>> b set(['a', 'q', 'i', 'l', 'o']) >>> a | b #可以有两种方式,结果一样 set(['a', 'i', 'l', 'o', 'q', 's', 'r', 'w']) >>> a.union(b) set(['a', 'i', 'l', 'o', 'q', 's', 'r', 'w'])
A、B的交集,即A、B所公有的元素,如下图所示

>>> a set(['q', 'i', 's', 'r', 'w']) >>> b set(['a', 'q', 'i', 'l', 'o']) >>> a & b #两种方式,等价 set(['q', 'i']) >>> a.intersection(b) set(['q', 'i'])
我在实验的时候,顺手敲了下面的代码,出现的结果如下,看官能解释一下吗?(思考题)
>>> a and b set(['a', 'q', 'i', 'l', 'o'])
A相对B的差(补),即A相对B不同的部分元素,如下图所示

>>> a set(['q', 'i', 's', 'r', 'w']) >>> b set(['a', 'q', 'i', 'l', 'o']) >>> a - b set(['s', 'r', 'w']) >>> a.difference(b) set(['s', 'r', 'w'])
-A、B的对称差集,如下图所示
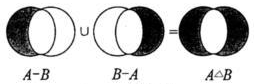
>>> a set(['q', 'i', 's', 'r', 'w']) >>> b set(['a', 'q', 'i', 'l', 'o']) >>> a.symmetric_difference(b) set(['a', 'l', 'o', 's', 'r', 'w'])
以上是集合的基本运算。在编程中,如果用到,可以用前面说的方法查找。不用死记硬背。