本文主要研究的是使用Python+pillow绘制矩阵盖尔圆的一个实例，具体如下。

盖尔圆是矩阵特征值估计时常用的方法之一，其定义为：

与盖尔圆有关的两个定理为：

定理1：矩阵A的所有特征值均落在它的所有盖尔圆的并集之中。

定理2：将矩阵A的全体盖尔圆的并集按连通部分分成若干个子集，（一个子集由完全连通的盖尔圆组成，不同子集没有相连通的部分），对每个子集，若它恰好由K个盖尔圆组成，则该子集中恰好包含A的K个特征值。

与盖尔圆定理有关的几个推论为：

推论1：孤立盖尔圆中恰好包含一个特征值。

推论2：实矩阵的孤立盖尔圆恰好包含一个实特征值。

推论3：盖尔圆方法中盖尔圆半径可以按列求和。（因为方阵转置后特征值不变）

下面的代码使用Python+pillow绘制给定矩阵的盖尔圆：

当输入矩阵[[10,20,30],[30,40,50],[50,65,70]]时，得到的图形如下：

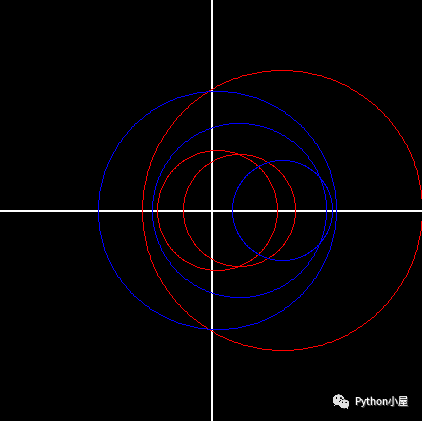
当输入矩阵[[6,27,33],[39,28,17],[80,60,71]]时，得到的图形如下：

总结

以上就是本文关于python+pillow绘制矩阵盖尔圆简单实例的全部内容，希望对大家有所帮助。感兴趣的朋友可以继续参阅本站其他相关专题，如有不足之处，欢迎留言指出。感谢朋友们对本站的支持！