Python基于Tkinter模块实现的弹球小游戏
本文实例讲述了Python基于Tkinter模块实现的弹球小游戏。分享给大家供大家参考,具体如下:
#!usr/bin/python
#-*- coding:utf-8 -*-
from Tkinter import *
import Tkinter
import random
import time
#创建小球的类
class Ball:
def __init__(self,canvas,paddle,color): #参数:画布,球拍和颜色
self.canvas = canvas
self.paddle = paddle
self.id = canvas.create_oval(10,10,25,25,fill = color) #参数:左上角坐标(x1,y1),右下角坐标(x2,y2),填充色
self.canvas.move(self.id,245,100) #把椭圆形移到画布的中心(245,100)
starts = [-3,-2,-1,1,2,3] #用一个列表随机一个小球的初始横向 X 坐标
random.shuffle(starts) #利用shuffle函数使starts列表混排一下,这样starts[0]就是列表中的随机值
self.x = starts[0] #所以X可能是以列表中的任意一个值开始的
self.y = -2 #初始的竖直方向运动的速度
self.canvas_height = self.canvas.winfo_height() #调用画布上的winfo_height函数来获取画布当前的高度
self.canvas_width = self.canvas.winfo_width() #保证小球不会从屏幕的两边消失,把画布的宽度保存到一个新的对象变量canvas_width中
self.hit_bottom =False
def hit_paddle(self,pos): #包含小球的当前坐标
paddle_pos = self.canvas.coords(self.paddle.id) #得到拍子的坐标,并把它们放到变量paddle_pos中
#pos[2]包含了小球的右侧X坐标,pos[0]包含了小球左侧的X坐标
if pos[2] >= paddle_pos[0] and pos[0] <=paddle_pos[2]: #如果小球的右侧大于球拍的左侧,并且小球的左侧小于球拍的右侧
#pos[3]表示小球的底部(此处判断小球的底部是否在球拍的顶部和底部之间,注:坐标从上到下是逐渐变大的,零点在上面)
if pos[3] >=paddle_pos[1] and pos[3] <= paddle_pos[3]:#可以理解为,第一个if判断和球拍的长那个面是否碰撞,第二个是侧面
return True
return False
def draw(self):
self.canvas.move(self.id,self.x,self.y)
pos = self.canvas.coords(self.id) #coords函数通过ID来返回当前画布上任何画好的东西的当前X和Y坐标
if pos[1] <=0: #coords函数返回一个由四个数字组成的列表来表示坐标(椭圆的左上角坐标和右下角的)
self.y=2#判断是否撞击到顶面
if pos[3] >=self.canvas_height:#判断小球是否撞到了屏幕的底部,如果小球一旦碰到了画布的底端,游戏就结束了i
self.hit_bottom = True
print"你输了!"
if self.hit_paddle(pos) == True: #hit_paddle()函数是用来判断小球是否撞击到球拍(如果撞到了就改变方向运动"-"代表反向,2代表速度)
self.y = -2
if pos[0] <=0:#最后两个if判断小球是否撞到了画布的左侧和右侧
self.x = 2
if pos[2] >= self.canvas_width:
self.x = -2
#球拍类
class Paddle:
def __init__(self,canvas,color):
self.canvas = canvas
self.id = canvas.create_rectangle(0,0,100,10,fill = color) #创建一个长方形球拍
self.canvas.move(self.id,200,300)#把球拍的坐标移到(200,300)横向200像素,纵向300像素
self.x =0
self.canvas_width = self.canvas.winfo_width() #保存画布宽度的变量
self.canvas.bind_all('<KeyPress-Left>',self.turn_left)#把turn_left()函数绑定到左方向键上
self.canvas.bind_all('<KeyPress-Right>',self.turn_right)#把turn_right()函数班规定到右方向键上
def draw(self):
self.canvas.move(self.id,self.x,0) #在x的方向上移动球拍
pos =self.canvas.coords(self.id)#获得球拍的坐标
if pos[0] <=0:#如果球拍运动到左边缘的时候,就让球拍停止运动,以下的elif道理相同
self.x = 0
elif pos[2] >= self.canvas_width:
self.x =0
def turn_left(self,evt): #移动球拍向左
self.x =-2
def turn_right(self,evt):#向右
self.x =2
t = Tkinter.Tk()
t.title("www.jb51.net Game") #用t对象中的title函数给窗口加一个标题,t对象是由t=Tk()创建的
t.resizable(0,0)#规定窗口不可调,两个参数0,0,表示在水平和竖直方向上都不可改变
t.wm_attributes("-topmost",1)#调用wm_attributes来告诉tkinter把包含我们画布的窗口放到所有其他窗口之前(-topmost)
canvas = Canvas(t,width=500,height=400,bd=0,highlightthickness=0)
canvas.pack()#按前一行给出的宽度和高度的参数来调整自身大小
t.update()#做好初始化
paddle = Paddle(canvas,'blue')
ball = Ball(canvas,paddle,'red')
while 1:
if ball.hit_bottom ==False:
ball.draw()
paddle.draw()
else:
break
t.update_idletasks()
t.update()#快速更新画布
time.sleep(0.01)
t.mainloop()
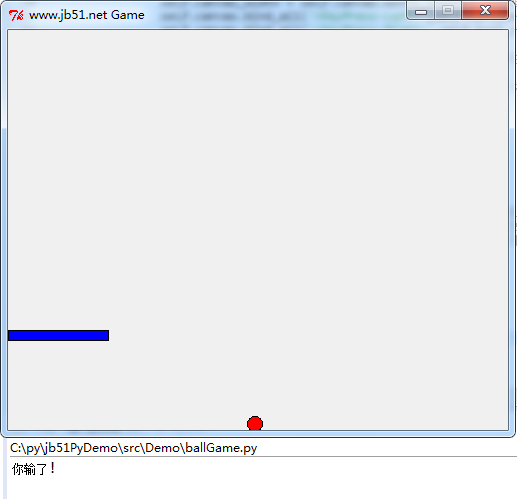
本机测试结果如下:
更多关于Python相关内容可查看本站专题:《Python游戏开发技巧总结》、《Python数据结构与算法教程》、《Python Socket编程技巧总结》、《Python函数使用技巧总结》、《Python字符串操作技巧汇总》、《Python入门与进阶经典教程》及《Python文件与目录操作技巧汇总》
希望本文所述对大家Python程序设计有所帮助。