python实现狄克斯特拉算法
一、简介
是从一个顶点到其余各顶点的最短路径算法,解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止
二、步骤
(1) 找出“最便宜”的节点,即可在最短时间内到达的节点。
(2) 更新该节点的邻居的开销,其含义将稍后介绍。
(3) 重复这个过程,直到对图中的每个节点都这样做了。
(4) 计算最终路径。
三、图解
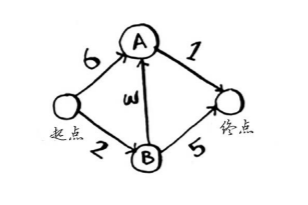
上图中包括5个节点,箭头表示方向,线上的数字表示消耗时间。
首先根据上图做出一个初始表(父节点代表从哪个节点到达该节点):
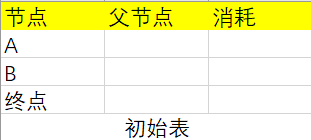
然后从“起点”开始,根据图中的信息更新一下表,由于从“起点”不能直接到达“终点”节点,所以耗时为∞(无穷大):
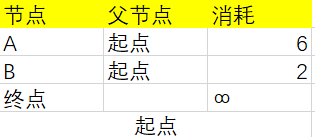
有了这个表我们可以根据算法的步骤往下进行了。
第一步:找出“最便宜”的节点,这里是节点B:
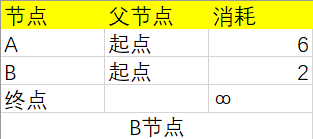
第二步:更新该节点的邻居的开销,根据图从B出发可以到达A和“终点”节点,B目前的消耗2+B到A的消耗3=5,5小于原来A的消耗6,所以更新节点A相关的行:
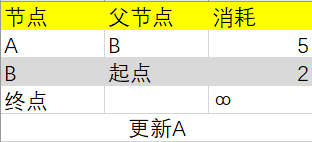
同理,B目前消耗2+B到End的消耗5=7,小于∞,更新“终点”节点行:
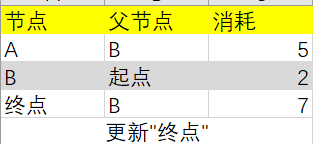
B节点关联的节点已经更新完成,所以B节点不在后面的更新范围之内了:
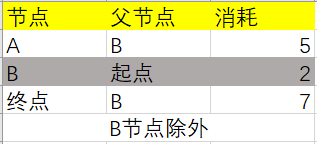
找到下一个消耗最小的节点,那就是A节点:
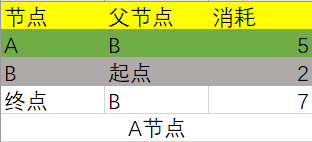
根据A节点的消耗更新关联节点,只有End节点行被更新了:
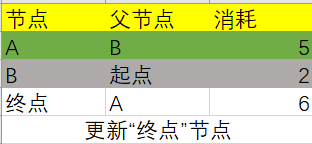
这时候A节点也不在更新节点范围之内了:
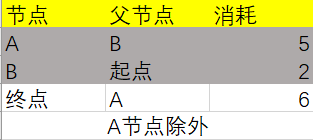
最终表的数据如下:
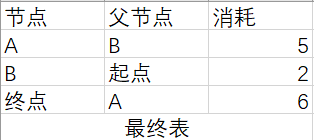
根据最终表,从“起点”到“终点”的最少消耗是6,路径是起点->B->A->终点.
四、代码实现
# -*-coding:utf-8-*-
# 用散列表实现图的关系
# 创建节点的开销表,开销是指从"起点"到该节点的权重
graph = {}
graph["start"] = {}
graph["start"]["a"] = 6
graph["start"]["b"] = 2
graph["a"] = {}
graph["a"]["end"] = 1
graph["b"] = {}
graph["b"]["a"] = 3
graph["b"]["end"] = 5
graph["end"] = {}
# 无穷大
infinity = float("inf")
costs = {}
costs["a"] = 6
costs["b"] = 2
costs["end"] = infinity
# 父节点散列表
parents = {}
parents["a"] = "start"
parents["b"] = "start"
parents["end"] = None
# 已经处理过的节点,需要记录
processed = []
# 找到开销最小的节点
def find_lowest_cost_node(costs):
# 初始化数据
lowest_cost = infinity
lowest_cost_node = None
# 遍历所有节点
for node in costs:
# 该节点没有被处理
if not node in processed:
# 如果当前节点的开销比已经存在的开销小,则更新该节点为开销最小的节点
if costs[node] < lowest_cost:
lowest_cost = costs[node]
lowest_cost_node = node
return lowest_cost_node
# 找到最短路径
def find_shortest_path():
node = "end"
shortest_path = ["end"]
while parents[node] != "start":
shortest_path.append(parents[node])
node = parents[node]
shortest_path.append("start")
return shortest_path
# 寻找加权的最短路径
def dijkstra():
# 查询到目前开销最小的节点
node = find_lowest_cost_node(costs)
# 只要有开销最小的节点就循环(这个while循环在所有节点都被处理过后结束)
while node is not None:
# 获取该节点当前开销
cost = costs[node]
# 获取该节点相邻的节点
neighbors = graph[node]
# 遍历当前节点的所有邻居
for n in neighbors.keys():
# 计算经过当前节点到达相邻结点的开销,即当前节点的开销加上当前节点到相邻节点的开销
new_cost = cost + neighbors[n]
# 如果经当前节点前往该邻居更近,就更新该邻居的开销
if new_cost < costs[n]:
costs[n] = new_cost
#同时将该邻居的父节点设置为当前节点
parents[n] = node
# 将当前节点标记为处理过
processed.append(node)
# 找出接下来要处理的节点,并循环
node = find_lowest_cost_node(costs)
# 循环完毕说明所有节点都已经处理完毕
shortest_path = find_shortest_path()
shortest_path.reverse()
print(shortest_path)
# 测试
dijkstra()
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持【听图阁-专注于Python设计】。