详解python实现小波变换的一个简单例子
最近工作需要,看了一下小波变换方面的东西,用python实现了一个简单的小波变换类,将来可以用在工作中。
简单说几句原理,小波变换类似于傅里叶变换,都是把函数用一组正交基函数展开,选取不同的基函数给出不同的变换。例如傅里叶变换,选择的是sin和cos,或者exp(ikx)这种复指数函数;而小波变换,选取基函数的方式更加灵活,可以根据要处理的数据的特点(比如某一段上信息量比较多),在不同尺度上采用不同的频宽来对已知信号进行分解,从而尽可能保留多一点信息,同时又避免了原始傅里叶变换的大计算量。以下计算采用的是haar基,它把函数分为2段(A1和B1,但第一次不分),对第一段内相邻的2个采样点进行变换(只考虑A1),变换矩阵为
sqrt(0.5) sqrt(0.5)
sqrt(0.5) -sqrt(0.5)
变换完之后,再把第一段(A1)分为两段,同样对相邻的点进行变换,直到无法再分。
下面直接上代码
Wavelet.py
import math
class wave:
def __init__(self):
M_SQRT1_2 = math.sqrt(0.5)
self.h1 = [M_SQRT1_2, M_SQRT1_2]
self.g1 = [M_SQRT1_2, -M_SQRT1_2]
self.h2 = [M_SQRT1_2, M_SQRT1_2]
self.g2 = [M_SQRT1_2, -M_SQRT1_2]
self.nc = 2
self.offset = 0
def __del__(self):
return
class Wavelet:
def __init__(self, n):
self._haar_centered_Init()
self._scratch = []
for i in range(0,n):
self._scratch.append(0.0)
return
def __del__(self):
return
def transform_inverse(self, list, stride):
self._wavelet_transform(list, stride, -1)
return
def transform_forward(self, list, stride):
self._wavelet_transform(list, stride, 1)
return
def _haarInit(self):
self._wave = wave()
self._wave.offset = 0
return
def _haar_centered_Init(self):
self._wave = wave()
self._wave.offset = 1
return
def _wavelet_transform(self, list, stride, dir):
n = len(list)
if (len(self._scratch) < n):
print("not enough workspace provided")
exit()
if (not self._ispower2(n)):
print("the list size is not a power of 2")
exit()
if (n < 2):
return
if (dir == 1): # 正变换
i = n
while(i >= 2):
self._step(list, stride, i, dir)
i = i>>1
if (dir == -1): # 逆变换
i = 2
while(i <= n):
self._step(list, stride, i, dir)
i = i << 1
return
def _ispower2(self, n):
power = math.log(n,2)
intpow = int(power)
intn = math.pow(2,intpow)
if (abs(n - intn) > 1e-6):
return False
else:
return True
def _step(self, list, stride, n, dir):
for i in range(0, len(self._scratch)):
self._scratch[i] = 0.0
nmod = self._wave.nc * n
nmod -= self._wave.offset
n1 = n - 1
nh = n >> 1
if (dir == 1): # 正变换
ii = 0
i = 0
while (i < n):
h = 0
g = 0
ni = i + nmod
for k in range(0, self._wave.nc):
jf = n1 & (ni + k)
h += self._wave.h1[k] * list[stride*jf]
g += self._wave.g1[k] * list[stride*jf]
self._scratch[ii] += h
self._scratch[ii + nh] += g
i += 2
ii += 1
if (dir == -1): # 逆变换
ii = 0
i = 0
while (i < n):
ai = list[stride*ii]
ai1 = list[stride*(ii+nh)]
ni = i + nmod
for k in range(0, self._wave.nc):
jf = n1 & (ni + k)
self._scratch[jf] += self._wave.h2[k] * ai + self._wave.g2[k] * ai1
i += 2
ii += 1
for i in range(0, n):
list[stride*i] = self._scratch[i]
测试代码如下:
test.py
import math
import Wavelet
waveletn = 256
waveletnc = 20 #保留的分量数
wavelettest = Wavelet.Wavelet(waveletn)
waveletorigindata = []
waveletdata = []
for i in range(0, waveletn):
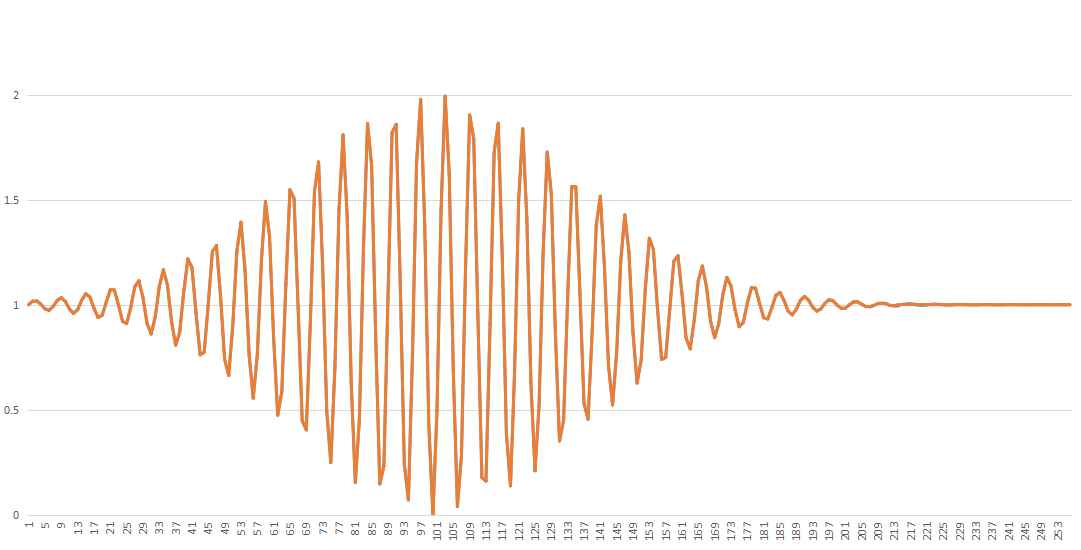
waveletorigindata.append(math.sin(i)*math.exp(-math.pow((i-100)/50,2))+1)
waveletdata.append(waveletorigindata[-1])
Wavelet.wavelettest.transform_forward(waveletdata, 1)
newdata = sorted(waveletdata, key = lambda ele: abs(ele), reverse=True)
for i in range(waveletnc, waveletn): # 筛选出前 waveletnc个分量保留
for j in range(0, waveletn):
if (abs(newdata[i] - waveletdata[j]) < 1e-6):
waveletdata[j] = 0.0
break
Wavelet.wavelettest.transform_inverse(waveletdata, 1)
waveleterr = 0.0
for i in range(0, waveletn):
print(waveletorigindata[i], ",", waveletdata[i])
waveleterr += abs(waveletorigindata[i] - waveletdata[i])/abs(waveletorigindata[i])
print("error: ", waveleterr/waveletn)
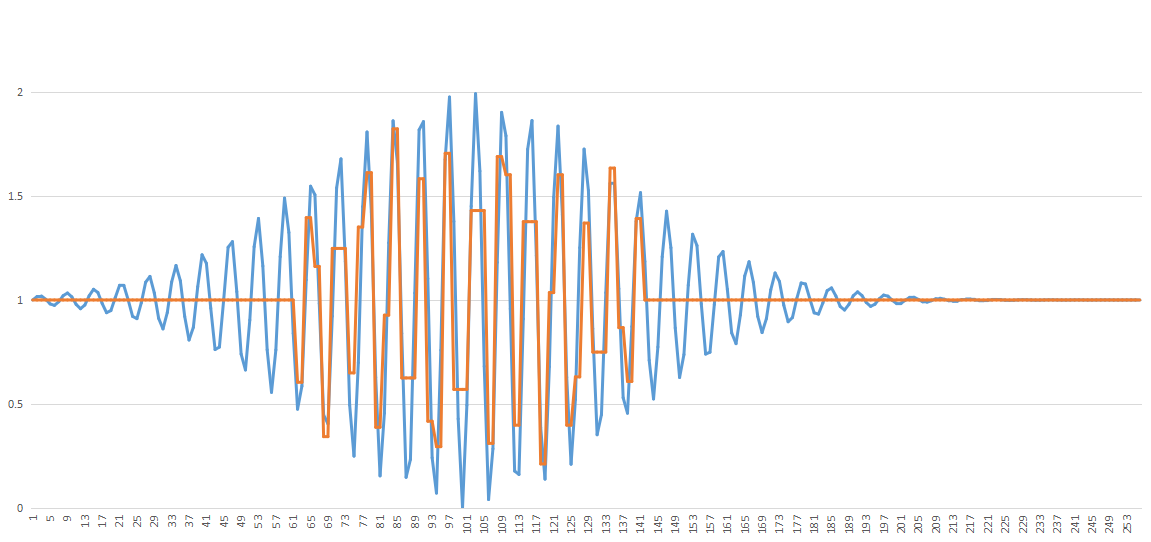
当waveletnc = 20时,可得到下图,误差大约为2.1
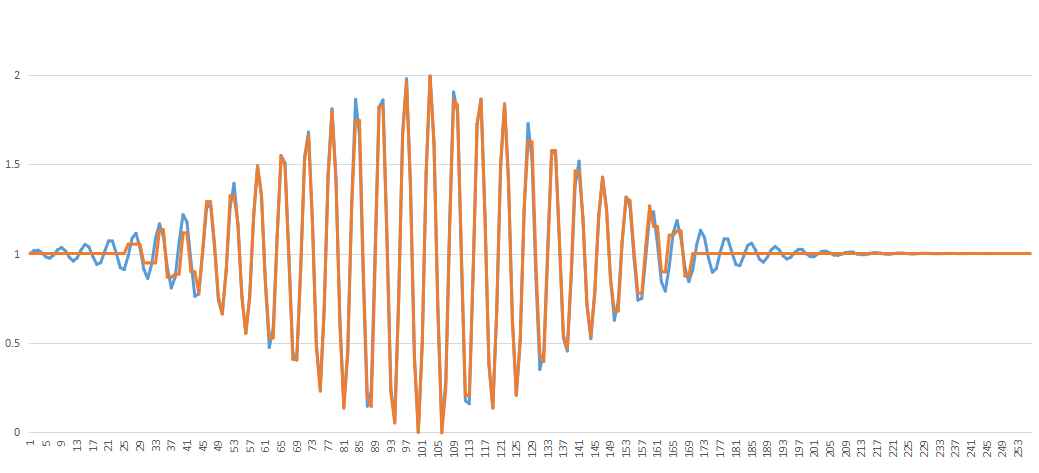
当waveletnc = 100时,则为下图,误差大约为0.04
当waveletnc = 200时,得到下图,误差大约为0.0005
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持【听图阁-专注于Python设计】。