python实现差分隐私Laplace机制详解
Laplace分布定义:

下面先给出Laplace分布实现代码:
import matplotlib.pyplot as plt
import numpy as np
def laplace_function(x,beta):
result = (1/(2*beta)) * np.e**(-1*(np.abs(x)/beta))
return result
#在-5到5之间等间隔的取10000个数
x = np.linspace(-5,5,10000)
y1 = [laplace_function(x_,0.5) for x_ in x]
y2 = [laplace_function(x_,1) for x_ in x]
y3 = [laplace_function(x_,2) for x_ in x]
plt.plot(x,y1,color='r',label='beta:0.5')
plt.plot(x,y2,color='g',label='beta:1')
plt.plot(x,y3,color='b',label='beta:2')
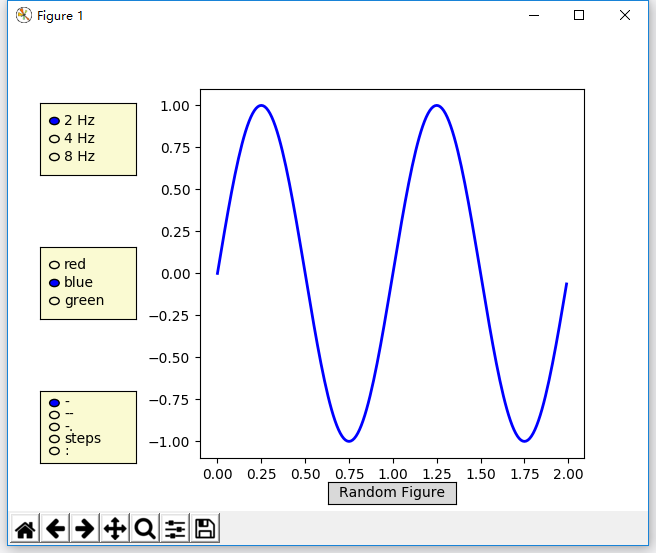
plt.title("Laplace distribution")
plt.legend()
plt.show()
效果图如下:

接下来给出Laplace机制实现:

Laplace机制,即在操作函数结果中加入服从Laplace分布的噪声。
Laplace概率密度函数Lap(x|b)=1/2b exp(-|x|/b)正比于exp(-|x|/b)。
import numpy as np def noisyCount(sensitivety,epsilon): beta = sensitivety/epsilon u1 = np.random.random() u2 = np.random.random() if u1 <= 0.5: n_value = -beta*np.log(1.-u2) else: n_value = beta*np.log(u2) print(n_value) return n_value def laplace_mech(data,sensitivety,epsilon): for i in range(len(data)): data[i] += noisyCount(sensitivety,epsilon) return data if __name__ =='__main__': x = [1.,1.,0.] sensitivety = 1 epsilon = 1 data = laplace_mech(x,sensitivety,epsilon) for j in data: print(j)
以上这篇python实现差分隐私Laplace机制详解就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持【听图阁-专注于Python设计】。