Python基于回溯法子集树模板解决取物搭配问题实例
本文实例讲述了Python基于回溯法子集树模板解决取物搭配问题。分享给大家供大家参考,具体如下:
问题
有5件不同的上衣,3条不同的裤子,4顶不同的帽子,从中取出一顶帽子、一件上衣和一条裤子作为一种搭配,问有多少种不同的搭配?
分析
换个角度看,现有头、身、腿三个元素,每个元素都有各自的几种状态。
头元素有['帽1', '帽2', '帽3', '帽4']共4种状态,身元素有['衣1', '衣2', '衣3', '衣4', '衣5']共5种状态,腿元素有['裤1', '裤2', '裤3']共3种状态
从头开始,自上而下,遍历每个元素的所有状态。
解的长度是固定的。
这里特别注意:每个元素的状态数目不同!!!
套用子集树模板即可
代码
```python '''取物排列问题''' n = 3 # 3个元素
头、身、腿3个元素各自的状态空间
a = [['帽1', '帽2', '帽3', '帽4'], ['衣1', '衣2', '衣3', '衣4', '衣5'], ['裤1', '裤2', '裤3']] x = [0]*n # 一个解,长度固定,3元数组 X = [] # 一组解
冲突检测
def conflict(k): return False # 无冲突
套用子集树模板
def match(k): # 到达第k个元素
global n, a, x, X
if k >= n: # 超出最尾的元素
print(x)
#X.append(x[:]) # 保存(一个解)
else:
for i in a[k]: # 直接a[k],若间接则range(len(a[k]))。 遍历第k个元素的对应的所有选择状态,不同的元素状态数目不同
x[k] = i
if not conflict(k): # 剪枝
match(k+1)
测试
match(0) # 从头(第0个元素)开始
效果图
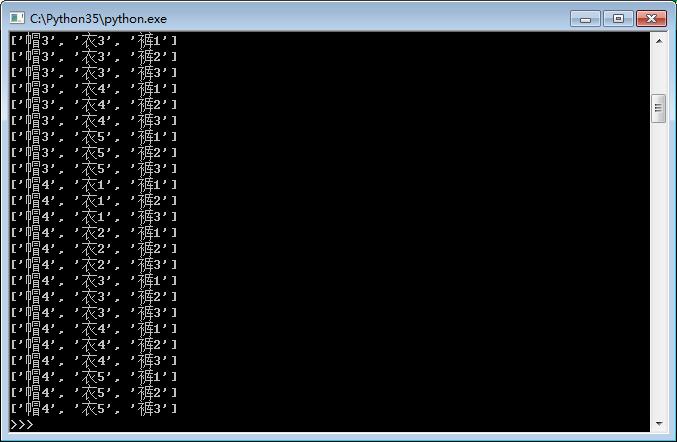
更多关于Python相关内容感兴趣的读者可查看本站专题:《Python数据结构与算法教程》、《Python函数使用技巧总结》、《Python字符串操作技巧汇总》及《Python入门与进阶经典教程》
希望本文所述对大家Python程序设计有所帮助。


