Python利用前序和中序遍历结果重建二叉树的方法
本文实例讲述了Python利用前序和中序遍历结果重建二叉树的方法。分享给大家供大家参考,具体如下:
题目:输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
这道题比较容易,前序遍历的结果中,第一个结点一定是根结点,然后在中序遍历的结果中查找这个根结点,根结点左边的就是左子树,根结点右边的就是右子树,递归构造出左、右子树即可。示意图如图所示:
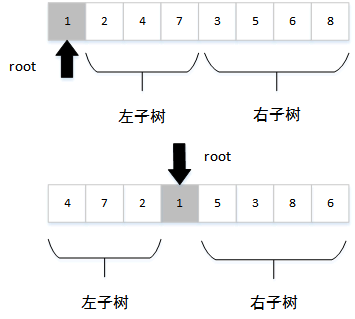
利用前序和中序遍历的结果重建二叉树
Python代码:
# coding: utf-8
'''
题目:输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
'''
class Node:
def __init__(self, data, left, right):
self.data = data
self.left = left
self.right = right
def construct_tree(pre_order, mid_order):
# 忽略参数合法性判断
if len(pre_order) == 0 :
return None
# 前序遍历的第一个结点一定是根结点
root_data = pre_order[0]
for i in range(0, len(mid_order)):
if mid_order[i] == root_data:
break
# 递归构造左子树和右子树
left = construct_tree(pre_order[1 : 1 + i], mid_order[:i])
right = construct_tree(pre_order[1 + i:], mid_order[i+1:])
return Node(root_data, left, right)
if __name__ == '__main__':
pre_order = [1, 2, 4, 7, 3, 5, 6, 8]
mid_order = [4, 7, 2, 1, 5, 3, 8, 6]
root = construct_tree(pre_order, mid_order)
print root.data
print root.left.data
print root.right.data
print root.left.left.data
print root.left.left.right.data
print root.right.right.left
print root.right.left.data
更多关于Python相关内容感兴趣的读者可查看本站专题:《Python数据结构与算法教程》、《Python Socket编程技巧总结》、《Python函数使用技巧总结》、《Python字符串操作技巧汇总》、《Python入门与进阶经典教程》及《Python文件与目录操作技巧汇总》
希望本文所述对大家Python程序设计有所帮助。