python中matplotlib实现最小二乘法拟合的过程详解
前言
最小二乘法Least Square Method,做为分类回归算法的基础,有着悠久的历史(由马里·勒让德于1806年提出)。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
下面这篇文章主要跟大家介绍了关于python中matplotlib实现最小二乘法拟合的相关内容,下面话不多说,来一起看看详细的介绍:
一、最小二乘法拟合直线
生成样本点
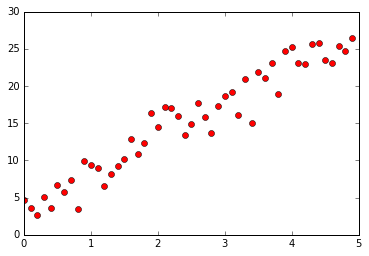
首先,我们在直线 y = 3 + 5x 附近生成服从正态分布的随机点,作为拟合直线的样本点。
import numpy as np import matplotlib.pyplot as plt # 在直线 y = 3 + 5x 附近生成随机点 X = np.arange(0, 5, 0.1) Z = [3 + 5 * x for x in X] Y = [np.random.normal(z, 0.5) for z in Z] plt.plot(X, Y, 'ro') plt.show()
样本点如图所示:
拟合直线
设 y = a0 + a1*x,我们利用最小二乘法的正则方程组来求解未知系数 a0 与 a1。
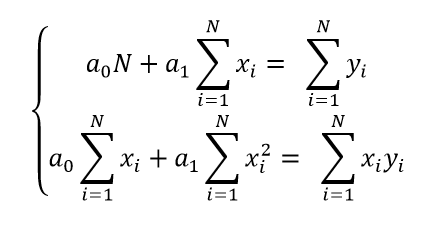
numpy 的 linalg 模块中有一个 solve 函数,它可以根据方程组的系数矩阵和方程右端构成的向量来求解未知量。
def linear_regression(x, y): N = len(x) sumx = sum(x) sumy = sum(y) sumx2 = sum(x**2) sumxy = sum(x*y) A = np.mat([[N, sumx], [sumx, sumx2]]) b = np.array([sumy, sumxy]) return np.linalg.solve(A, b) a0, a1 = linear_regression(X, Y)
绘制直线
此时,我们已经得到了拟合后的直线方程系数 a0 和 a1。接下来,我们绘制出这条直线,并与样本点做对比。
# 生成拟合直线的绘制点
_X = [0, 5]
_Y = [a0 + a1 * x for x in _X]
plt.plot(X, Y, 'ro', _X, _Y, 'b', linewidth=2)
plt.title("y = {} + {}x".format(a0, a1))
plt.show()
拟合效果如下:
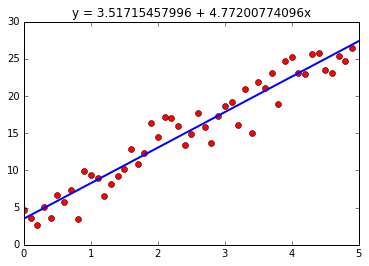
二、最小二乘法拟合曲线
生成样本点
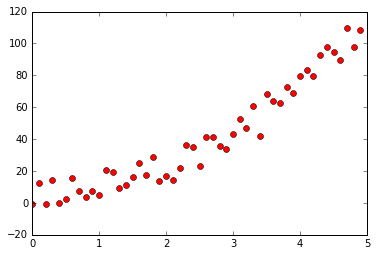
与生成直线样本点相同,我们在曲线 y = 2 + 3x + 4x^2 附近生成服从正态分布的随机点,作为拟合曲线的样本点。
import numpy as np import matplotlib.pyplot as plt # y = 2 + 3x + 4x^2 X = np.arange(0, 5, 0.1) Z = [2 + 3 * x + 4 * x ** 2 for x in X] Y = np.array([np.random.normal(z,3) for z in Z]) plt.plot(X, Y, 'ro') plt.show()
样本点如图所示:
拟合曲线
设该曲线的方程为 y = a0 + a1*x + a2*x^2,同样,我们通过正则方程组来求解未知量 a0、a1 和 a2。
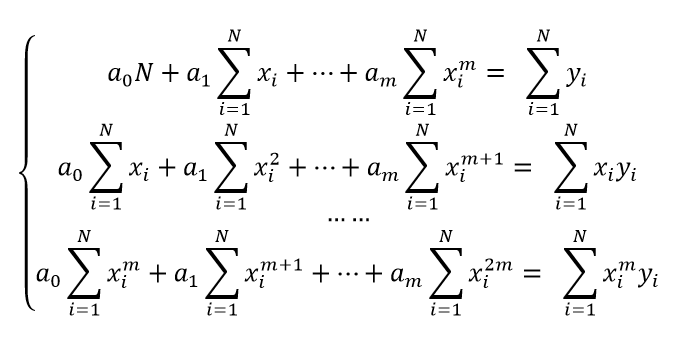
# 生成系数矩阵A def gen_coefficient_matrix(X, Y): N = len(X) m = 3 A = [] # 计算每一个方程的系数 for i in range(m): a = [] # 计算当前方程中的每一个系数 for j in range(m): a.append(sum(X ** (i+j))) A.append(a) return A # 计算方程组的右端向量b def gen_right_vector(X, Y): N = len(X) m = 3 b = [] for i in range(m): b.append(sum(X**i * Y)) return b A = gen_coefficient_matrix(X, Y) b = gen_right_vector(X, Y) a0, a1, a2 = np.linalg.solve(A, b)
绘制曲线
我们根据求得的曲线方程,绘制出曲线的图像。
# 生成拟合曲线的绘制点
_X = np.arange(0, 5, 0.1)
_Y = np.array([a0 + a1*x + a2*x**2 for x in _X])
plt.plot(X, Y, 'ro', _X, _Y, 'b', linewidth=2)
plt.title("y = {} + {}x + {}$x^2$ ".format(a0, a1, a2))
plt.show()
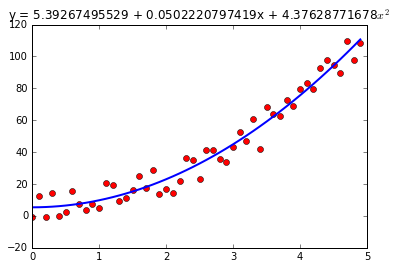
拟合效果如下:
总结
以上就是这篇文章的全部内容了,希望本文的内容对大家的学习或者工作能带来一定的帮助,如果有疑问大家可以留言交流,谢谢大家对【听图阁-专注于Python设计】的支持。
