Python用户推荐系统曼哈顿算法实现完整代码
出租车几何或曼哈顿距离(Manhattan Distance)是由十九世纪的赫尔曼·闵可夫斯基所创词汇 ,是种使用在几何度量空间的几何学用语,用以标明两个点在标准坐标系上的绝对轴距总和。
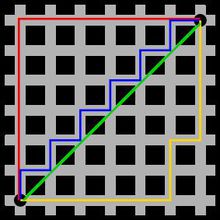
图中红线代表曼哈顿距离,绿色代表欧氏距离,也就是直线距离,而蓝色和黄色代表等价的曼哈顿距离。曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离,即d(i,j)=|xi-xj|+|yi-yj|。对于一个具有正南正北、正东正西方向规则布局的城镇街道,从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离,因此,曼哈顿距离又称为出租车距离。曼哈顿距离不是距离不变量,当坐标轴变动时,点间的距离就会不同。曼哈顿距离示意图在早期的计算机图形学中,屏幕是由像素构成,是整数,点的坐标也一般是整数,原因是浮点运算很昂贵,很慢而且有误差,如果直接使用AB的欧氏距离(欧几里德距离:在二维和三维空间中的欧氏距离的就是两点之间的距离),则必须要进行浮点运算,如果使用AC和CB,则只要计算加减法即可,这就大大提高了运算速度,而且不管累计运算多少次,都不会有误差。
Python用户推荐系统曼哈顿算法实现
#-*- coding: utf-8 -*-
import codecs
from math import sqrt
users = {"Angelica": {"Blues Traveler": 3.5, "Broken Bells": 2.0, "Norah Jones": 4.5, "Phoenix": 5.0, "Slightly Stoopid": 1.5, "The Strokes": 2.5, "Vampire Weekend": 2.0},
"Bill":{"Blues Traveler": 2.0, "Broken Bells": 3.5, "Deadmau5": 4.0, "Phoenix": 2.0, "Slightly Stoopid": 3.5, "Vampire Weekend": 3.0},
"Chan": {"Blues Traveler": 5.0, "Broken Bells": 1.0, "Deadmau5": 1.0, "Norah Jones": 3.0, "Phoenix": 5, "Slightly Stoopid": 1.0},
"Dan": {"Blues Traveler": 3.0, "Broken Bells": 4.0, "Deadmau5": 4.5, "Phoenix": 3.0, "Slightly Stoopid": 4.5, "The Strokes": 4.0, "Vampire Weekend": 2.0},
"Hailey": {"Broken Bells": 4.0, "Deadmau5": 1.0, "Norah Jones": 4.0, "The Strokes": 4.0, "Vampire Weekend": 1.0},
"Jordyn": {"Broken Bells": 4.5, "Deadmau5": 4.0, "Norah Jones": 5.0, "Phoenix": 5.0, "Slightly Stoopid": 4.5, "The Strokes": 4.0, "Vampire Weekend": 4.0},
"Sam": {"Blues Traveler": 5.0, "Broken Bells": 2.0, "Norah Jones": 3.0, "Phoenix": 5.0, "Slightly Stoopid": 4.0, "The Strokes": 5.0},
"Veronica": {"Blues Traveler": 3.0, "Norah Jones": 5.0, "Phoenix": 4.0, "Slightly Stoopid": 2.5, "The Strokes": 3.0}
}
# Python计算曼哈顿距离 www.iplaypy.com
def manhattan(rate1,rate2):
distance = 0
commonRating = False
for key in rate1:
if key in rate2:
distance+=abs(rate1[key]-rate2[key])
commonRating=True
if commonRating:
return distance
else:
return -1
# python返回最近距离用户
def computeNearestNeighbor(username,users):
distances = []
for key in users:
if key<>username:
distance = manhattan(users[username],users[key])
distances.append((distance,key))
distances.sort()
return distances
#推荐python实现
def recommend(username,users):
#获得最近用户的name
nearest = computeNearestNeighbor(username,users)[0][1]
recommendations =[]
#得到最近用户的推荐列表
neighborRatings = users[nearest]
for key in neighborRatings:
if not key in users[username]:
recommendations.append((key,neighborRatings[key]))
recommendations.sort(key=lambda rat:rat[1], reverse=True)
return recommendations
if __name__ == '__main__':
print recommend('Hailey', users)
总结
以上就是本文关于Python用户推荐系统曼哈顿算法实现完整代码的全部内容,希望对大家有所帮助。感兴趣的朋友可以继续参阅本站其他相关专题,如有不足之处,欢迎留言指出。感谢朋友们对本站的支持!
