Python基于最小二乘法实现曲线拟合示例
本文实例讲述了Python基于最小二乘法实现曲线拟合。分享给大家供大家参考,具体如下:
这里不手动实现最小二乘,调用scipy库中实现好的相关优化函数。
考虑如下的含有4个参数的函数式:
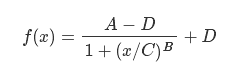
构造数据
import numpy as np from scipy import optimize import matplotlib.pyplot as plt def logistic4(x, A, B, C, D): return (A-D)/(1+(x/C)**B)+D def residuals(p, y, x): A, B, C, D = p return y - logisctic4(x, A, B, C, D) def peval(x, p): A, B, C, D = p return logistic4(x, A, B, C, D) A, B, C, D = .5, 2.5, 8, 7.3 x = np.linspace(0, 20, 20) y_true = logistic4(x, A, B, C, D) y_meas = y_true + 0.2 * np.random.randn(len(y_true))
调用工具箱函数,进行优化
p0 = [1/2]*4
plesq = optimize.leastsq(residuals, p0, args=(y_meas, x))
# leastsq函数的功能其实是根据误差(y_meas-y_true)
# 估计模型(也即函数)的参数
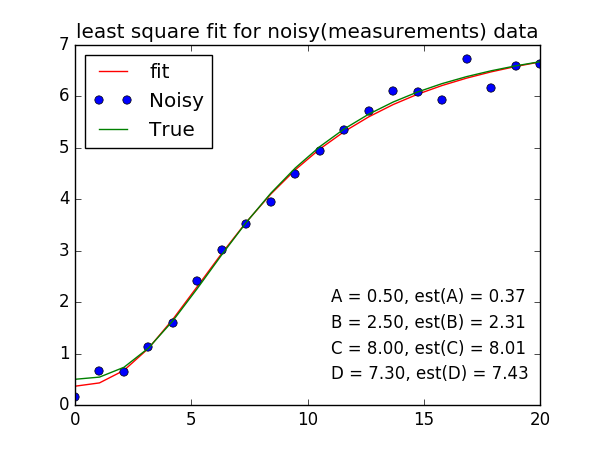
绘图
plt.figure(figsize=(6, 4.5))
plt.plot(x, peval(x, plesq[0]), x, y_meas, 'o', x, y_true)
plt.legend(['Fit', 'Noisy', 'True'], loc='upper left')
plt.title('least square for the noisy data (measurements)')
for i, (param, true, est) in enumerate(zip('ABCD', [A, B, C, D], plesq[0])):
plt.text(11, 2-i*.5, '{} = {:.2f}, est({:.2f}) = {:.2f}'.format(param, true, param, est))
plt.savefig('./logisitic.png')
plt.show()
PS:这里再为大家推荐两款相似的在线工具供大家参考:
在线多项式曲线及曲线函数拟合工具:
http://tools.jb51.net/jisuanqi/create_fun
在线绘制多项式/函数曲线图形工具:
http://tools.jb51.net/jisuanqi/fun_draw
更多关于Python相关内容感兴趣的读者可查看本站专题:《Python数学运算技巧总结》、《Python数据结构与算法教程》、《Python函数使用技巧总结》、《Python字符串操作技巧汇总》及《Python入门与进阶经典教程》
希望本文所述对大家Python程序设计有所帮助。