python实现傅里叶级数展开的实现
傅立叶级数的介绍我就不说了,自己也是应用为主,之前一直觉得很难懂,但最近通过自己编程实现了一些函数的傅立叶级数展开之后对傅立叶 级数展开的概念比较清楚了
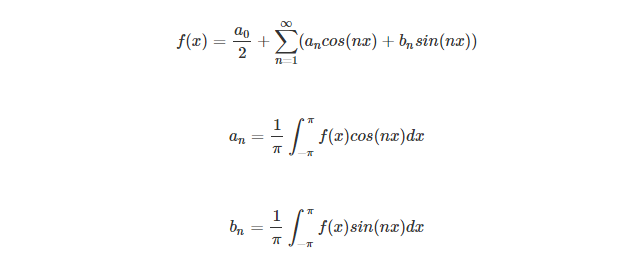
(1)函数如下
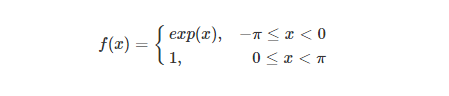
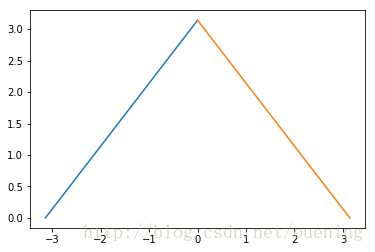
函数图象如下:
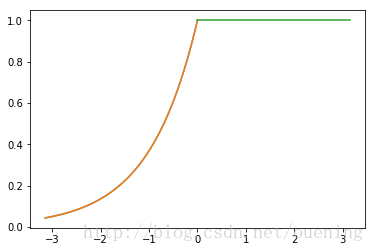
代码:
from pylab import *
x = mgrid[-10:10:0.02] # 这里类似于MATLAB用冒号产生步长为0.02的序列,但是语法和MATLAB不同
n = arange(1,1000)
def fourier_transform():
a0 = (1-exp(-pi))/pi+1
s=a0/2
for i in range(1,100,1):
s0 = ( (1-(-1)**i*exp(-pi))/(pi*(1+i**2))*cos(i*x)+1/pi*( (-i*(1-(-1)**i*exp(-pi)))/(1+i**2) + (1-(-1)**i)/i ) * sin(i*x) )
s=s+s0
plot(x,s,'orange',linewidth=0.6)
title('fourier_transform')
show()
fourier_transform()
结果如下:
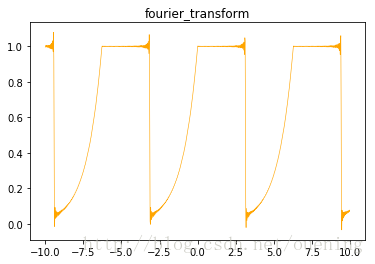
(2)
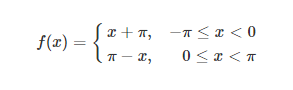
转换代码:
from pylab import *
def fourier1():
s=pi/2
for i in range(1,100,1):
s0 = 2/pi*(1-(-1)**i)/i**2 * cos(i*x)
s=s+s0
plot(x,s,'orange',linewidth=0.6)
title('fourier1')
show()
fourier1()
结果如下:
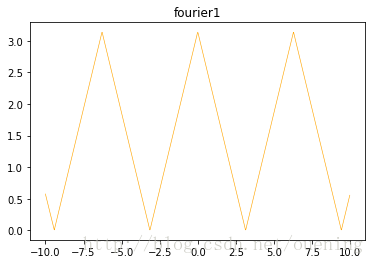
关于傅里叶级数展开的还有一些例子在我的另一篇博客/post/144196.htm也有讨论,通过以上的例子可以很好直观感受傅立叶级数的作用,在电气工程上对分析流经变压器的谐波分量、整流装置输出谐波等分析具有重要作用。
还有一点就是python的强大功能,利用for循环语句可以方便地实现级数展开的求和运算,自己感觉编程起来比MATLAB/Octave跟快
相关文章:Python实现快速傅里叶变换(FFT)
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持【听图阁-专注于Python设计】。
