TensorFlow实现iris数据集线性回归
本文将遍历批量数据点并让TensorFlow更新斜率和y截距。这次将使用Scikit Learn的内建iris数据集。特别地,我们将用数据点(x值代表花瓣宽度,y值代表花瓣长度)找到最优直线。选择这两种特征是因为它们具有线性关系,在后续结果中将会看到。本文将使用L2正则损失函数。
# 用TensorFlow实现线性回归算法
#----------------------------------
#
# This function shows how to use TensorFlow to
# solve linear regression.
# y = Ax + b
#
# We will use the iris data, specifically:
# y = Sepal Length
# x = Petal Width
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from sklearn import datasets
from tensorflow.python.framework import ops
ops.reset_default_graph()
# Create graph
sess = tf.Session()
# Load the data
# iris.data = [(Sepal Length, Sepal Width, Petal Length, Petal Width)]
iris = datasets.load_iris()
x_vals = np.array([x[3] for x in iris.data])
y_vals = np.array([y[0] for y in iris.data])
# 批量大小
batch_size = 25
# Initialize 占位符
x_data = tf.placeholder(shape=[None, 1], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
# 模型变量
A = tf.Variable(tf.random_normal(shape=[1,1]))
b = tf.Variable(tf.random_normal(shape=[1,1]))
# 增加线性模型,y=Ax+b
model_output = tf.add(tf.matmul(x_data, A), b)
# 声明L2损失函数,其为批量损失的平均值。
loss = tf.reduce_mean(tf.square(y_target - model_output))
# 声明优化器 学习率设为0.05
my_opt = tf.train.GradientDescentOptimizer(0.05)
train_step = my_opt.minimize(loss)
# 初始化变量
init = tf.global_variables_initializer()
sess.run(init)
# 批量训练遍历迭代
# 迭代100次,每25次迭代输出变量值和损失值
loss_vec = []
for i in range(100):
rand_index = np.random.choice(len(x_vals), size=batch_size)
rand_x = np.transpose([x_vals[rand_index]])
rand_y = np.transpose([y_vals[rand_index]])
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})
loss_vec.append(temp_loss)
if (i+1)%25==0:
print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)) + ' b = ' + str(sess.run(b)))
print('Loss = ' + str(temp_loss))
# 抽取系数
[slope] = sess.run(A)
[y_intercept] = sess.run(b)
# 创建最佳拟合直线
best_fit = []
for i in x_vals:
best_fit.append(slope*i+y_intercept)
# 绘制两幅图
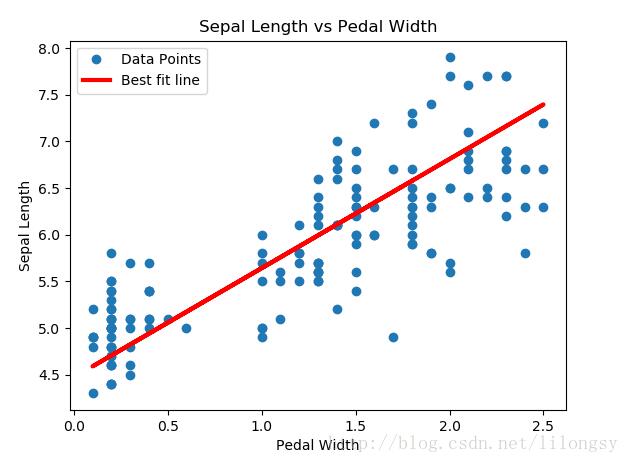
# 拟合的直线
plt.plot(x_vals, y_vals, 'o', label='Data Points')
plt.plot(x_vals, best_fit, 'r-', label='Best fit line', linewidth=3)
plt.legend(loc='upper left')
plt.title('Sepal Length vs Pedal Width')
plt.xlabel('Pedal Width')
plt.ylabel('Sepal Length')
plt.show()
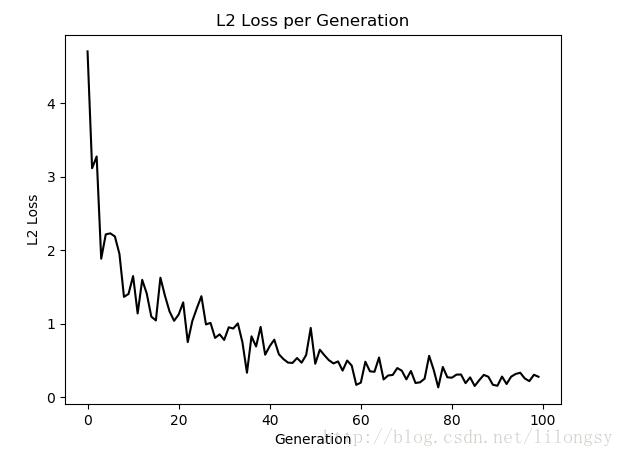
# Plot loss over time
# 迭代100次的L2正则损失函数
plt.plot(loss_vec, 'k-')
plt.title('L2 Loss per Generation')
plt.xlabel('Generation')
plt.ylabel('L2 Loss')
plt.show()
结果:
Step #25 A = [[ 1.93474162]] b = [[ 3.11190438]] Loss = 1.21364 Step #50 A = [[ 1.48641717]] b = [[ 3.81004381]] Loss = 0.945256 Step #75 A = [[ 1.26089203]] b = [[ 4.221035]] Loss = 0.254756 Step #100 A = [[ 1.1693294]] b = [[ 4.47258472]] Loss = 0.281654
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持【听图阁-专注于Python设计】。