python opencv实现图像边缘检测
本文利用python opencv进行图像的边缘检测,一般要经过如下几个步骤:
1、去噪
如cv2.GaussianBlur()等函数;
2、计算图像梯度
图像梯度表达的是各个像素点之间,像素值大小的变化幅度大小,变化较大,则可以认为是出于边缘位置,最多可简化为如下形式:
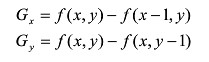
3、非极大值抑制
在获得梯度的方向和大小之后,应该对整幅图像做一个扫描,去除那些非边界上的点。对每一个像素进行检查,看这个点的梯度是不是周围具有相同梯度方向的点中最大的。如下图所示:
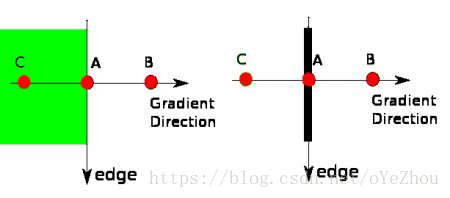
4、滞后阈值
现在要确定那些边界才是真正的边界。这时我们需要设置两个阈值:minVal 和maxVal。当图像的灰度梯度高于maxVal 时被认为是真的边界,那些低于minVal 的边界会被抛弃。如果介于两者之间的话,就要看这个点是否与某个被确定为真正的边界点相连,如果是就认为它也是边界点,如果不是就抛弃。如下图:

在Python Opencv接口中,提供了Canny函数,可以对图像进行一键执行边缘检测。
接下来,利用Canny函数进行边缘检测的实验。
Canny函数需要指定几个参数:
1、需要进行边缘检测的原图
2、阈值下限
3、阈值上限
我们为了能够看到不同阈值范围对边缘检测结果的影响,设置了两个滑动条,来分别表示阈值上下限。
完整代码如下:
# -*- coding: utf-8 -*-
"""
Created on Thu Sep 13 14:23:32 2018
@author: Leon
内容:
对图片进行边缘检测;
添加滑动条,可自由调整阈值上下限。
"""
import cv2
import numpy as np
def nothing(x):
pass
cv2.namedWindow('Canny',0)
# 创建滑动条
cv2.createTrackbar('minval','Canny',0,255,nothing)
cv2.createTrackbar('maxval','Canny',0,255,nothing)
img = cv2.imread('Tree.jpg',0)
# 高斯滤波去噪
img = cv2.GaussianBlur(img,(3,3),0)
edges =img
k=0
while(1):
key = cv2.waitKey(50) & 0xFF
if key == ord('q'):
break
# 读取滑动条数值
minval = cv2.getTrackbarPos('minval','Canny')
maxval = cv2.getTrackbarPos('maxval','Canny')
edges = cv2.Canny(img,minval,maxval)
# 拼接原图与边缘监测结果图
img_2 = np.hstack((img,edges))
cv2.imshow('Canny',img_2)
cv2.destroyAllWindows()
效果如图:
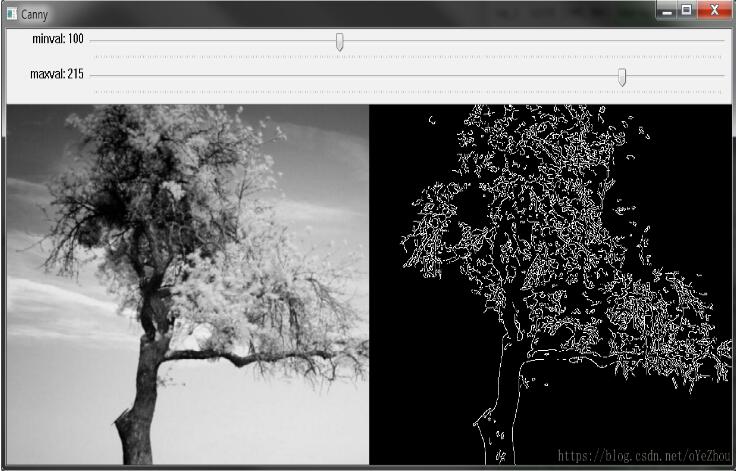
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持【听图阁-专注于Python设计】。