Python numpy线性代数用法实例解析
这篇文章主要介绍了Python numpy线性代数用法实例解析,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友可以参考下
numpy中线性代数用法
矩阵乘法
>>> import numpy as np
>>> x=np.array([[1,2,3],[4,5,6]])
>>> y=np.array([[7,8],[-1,7],[8,9]])
>>> x
array([[1, 2, 3],
[4, 5, 6]])
>>> y
array([[ 7, 8],
[-1, 7],
[ 8, 9]])
>>> x.dot(y)
array([[ 29, 49],
[ 71, 121]])
>>> np.dot(x,y)
array([[ 29, 49],
[ 71, 121]])
计算点积
>>> a=np.array([[1,2],[3,4]]) >>> b=np.array([[11,12],[12,13]]) >>> np.vdot(a,b) 123
计算的公式是
result=1*11+2*12+3*12+4*13
计算内积
>>> np.inner(np.array([1,2,3]),np.array([0,1,0])) 2
计算公式
result=1*0+2*1+3*0
计算行列式
>>> np.inner(np.array([1,2,3]),np.array([0,1,0])) 2 >>> a=np.array([[1,2],[3,4]]) >>> np.linalg.det(a) -2.0000000000000004
求线性方程的解
x + y + z = 6 2y + 5z = -4 2x + 5y - z = 27
矩阵表示
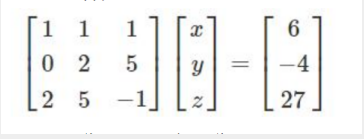
>>> import numpy as np
>>> a = np.array([[1,1,1],[0,2,5],[2,5,-1]])
>>> ainv = np.linalg.inv(a)#求矩阵的逆
>>> b = np.array([[6],[-4],[27]])
>>> x = np.linalg.solve(a,b)#求解需要A-1和B
>>> x
array([[ 5.],
[ 3.],
[-2.]])
>>>
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持【听图阁-专注于Python设计】。
