Python求解正态分布置信区间教程
正态分布和置信区间
正态分布(Normal Distribution)又叫高斯分布,是一种非常重要的概率分布。其概率密度函数的数学表达如下:

置信区间是对该区间能包含未知参数的可置信的程度的描述。
使用SciPy求解置信区间
import numpy as np import matplotlib.pyplot as plt from scipy import stats N = 10000 x = np.random.normal(0, 1, N) # ddof取值为1是因为在统计学中样本的标准偏差除的是(N-1)而不是N,统计学中的标准偏差除的是N # SciPy中的std计算默认是采用统计学中标准差的计算方式 mean, std = x.mean(), x.std(ddof=1) print(mean, std) # 计算置信区间 # 这里的0.9是置信水平 conf_intveral = stats.norm.interval(0.9, loc=mean, scale=std) print(conf_intveral)
输出如下:
0.0033541207210673997 0.9986647964318905 (-1.639303291798682, 1.6460115332408163)
这里的-1.639303291798682是置信上界,1.6460115332408163是置信下界,两个数值构成的区间就是置信区间
使用Matplotlib绘制正态分布密度曲线
# 绘制概率密度分布图 x = np.arange(-5, 5, 0.001) # PDF是概率密度函数 y = stats.norm.pdf(x, loc=mean, scale=std) plt.plot(x, y) plt.show()
这里的pdf()函数是Probability density function,就是本文最开始的那个公式
最后的输出图像如下,可以看到结果跟理论上的正太分布还是比较像的:
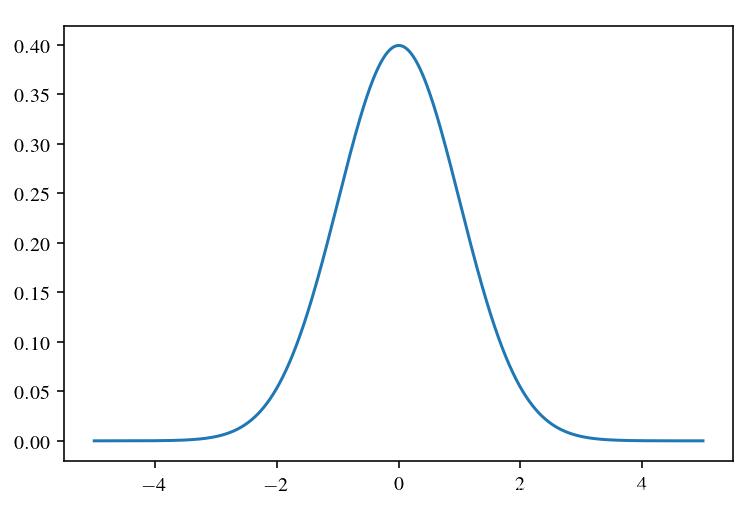
正态分布置信区间规律
函数曲线下68.268949%的面积在平均数左右的一个标准差范围内
函数曲线下95.449974%的面积在平均数左右两个标准差的范围内
函数曲线下99.730020%的面积在平均数左右三个标准差的范围内
函数曲线下99.993666%的面积在平均数左右四个标准差的范围内
以上这篇Python求解正态分布置信区间教程就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持【听图阁-专注于Python设计】。